こんな人におすすめの記事です。
- これまで何となくでTable1を描いてきた
- Table1をどう描くべきか教えてもらったことがない
こんなお悩みを解決します。
量的研究をやった人なら絶対に描いたことがあるTable 1。
その研究の対象者の特性を一枚で伝えるための表です。
このTable 1、実は奥が深い。
Table 1の役割は主に2つ。
- 研究の内的妥当性のアセスメント
- 研究の外的妥当性のアセスメント
要は「内的妥当性・外的妥当性が適切にアセスメントできるTable 1」が質の高いそれということになります。
じゃあ、それってどんなTable 1でしょうか？
どんな行・列を用意して、どこに、何を、どんな形式で入れ込めば良いのでしょう？
この記事ではTable 1のガイドライン論文をベースに、質の高いTable 1の描き方を解説していきます！
Table 1って当たり前のように描いてるけど、実はきちんと描き方を習う機会って多くないよね
本ブログは、私個人の責任で執筆され、所属する組織の見解を代表する物ではありません
Table 1の役割とは？
突然ですが、Table 1とはコイツ。
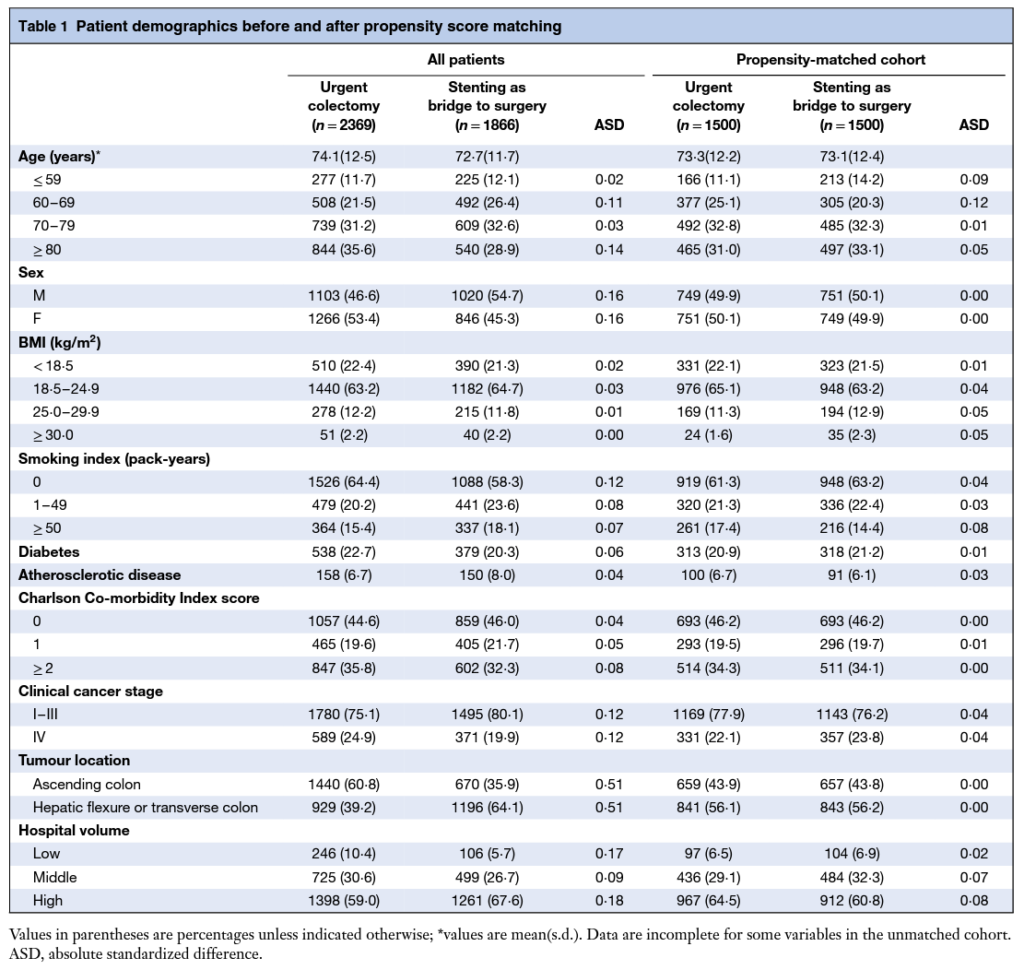
論文の表のうちで一番最初に出てくるやつですね。
Table 1の役割とはずばり、「Who is in this study？」という読者の質問に答えること。
もっと具体的にいうと、以下の2つの役割があります。
- その研究結果が他のポピュレーションに外挿可能であるかどうかをアセスメントする（外的妥当性）
- その研究結果にバイアスのリスクがどの程度あるかをアセスメントする（内的妥当性）
Table 1の構造について
Table 1を描く際に考えるべき点は次の2点です。
- 列
- 行
あたりまえの表の構成要素ですね。
ちなみにこちらは本記事が参考にする論文に掲載されているTable 1の構成になります。
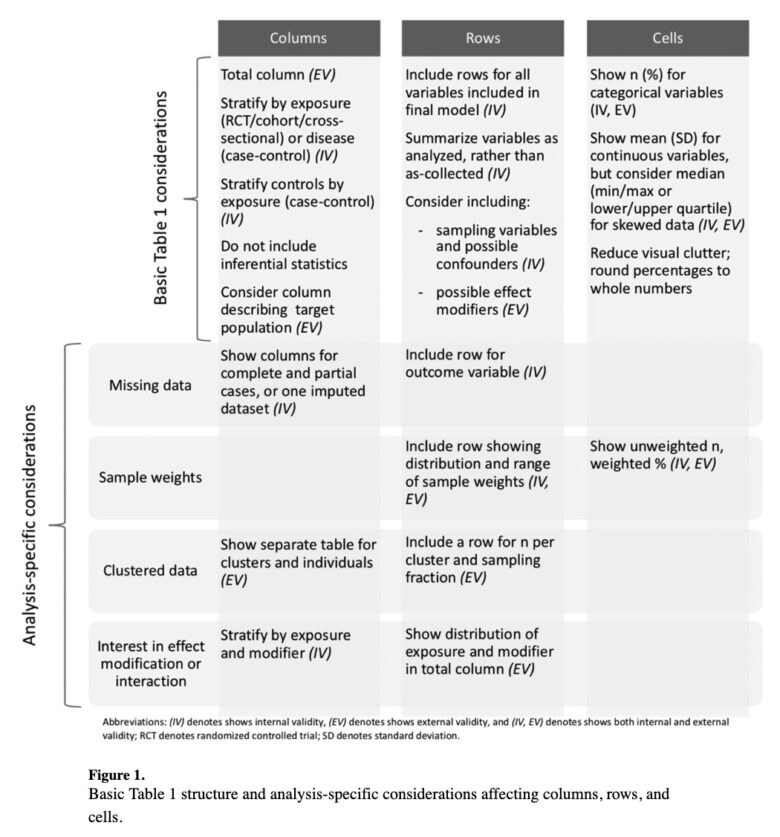
ではこれから、質の高いTable 1を描くためには列、行、セルのそれぞれにおいてどんなことを考えていけば良いのか、順に解説していきましょう。
質の高い列の描き方
列は英語でColumn、介入と非介入の2軸（RCTやコホート研究）、もしくはケースとコントロール（ケースコントロール研究）の2軸のグループ分けがよく行われます。
どちらのパターンを使うかで注意すべき点も変わります。
（私が医療大規模データベース研究を専門にしているからか）ケースコントロール研究を目にすることがあまりないので、ここではよりメジャーであるコホート研究のパターンをベースに解説していきます。
内的妥当性の観点から
内的妥当性をさらに分類すると、以下の3点に大きくアセスメントポイントが分類されます。
- 交絡バイアス
- 選択バイアス
- 測定バイアス
【交絡バイアス】
交絡バイアスは介入 vs 非介入（もしくは曝露）の2群間においてアウトカムの原因となる因子の分布がアンバランスであることで生じるバイアスです。
ですから端的に言えば、Table 1ではこの2群間においてそのような因子の分布がアンバランスになっていないかどうかを確かめる必要があります。
ここまではコモンセンスと言って良いでしょう。
よく議論になるのはここから先、「そのアンバランスを評価するためにP-valueを入れるべきかどうか」ということです。
疫学・統計学を学ばれている方であれば「あーはん？そんなん分かっとるわ」というところでしょうが、これは「入れるべきではない」というのが答えになります。
なぜなら、交絡因子の有無は前提となる変数間の因果関係の知識によって決められるべきものであり、「P値が有意だったから交絡因子になる」という性質のものではないからです。
本記事の主題ではないのでこれ以上の解説はしませんが、より詳細を知りたい方はここら辺の論文がおすすめです。
ご覧の通り、本記事がベースにしている論文でもTable 1にP値を入れておりません（Point 4がその解説です）。
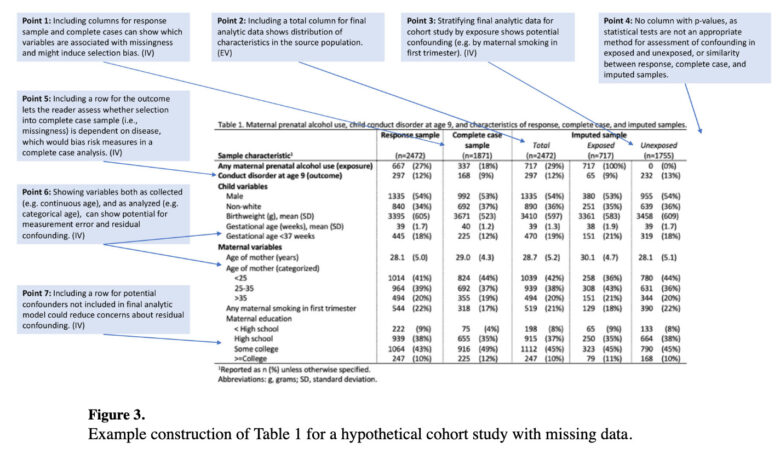
P値によって交絡の有無を判断するのではなく、先行研究や生物学的妥当性、臨床的妥当性などの観点から仮説として交絡因子を定義し、そしてTable 1では「その交絡因子の分布が2群間でどれだけ違っているか、そしてそのことが結果に与える影響はどの程度であるか」ということを思索すべきとされています。
【選択バイアス】
欠損により対象者が”選択”されることによって、選択バイアスが生じる可能性があります。
ですので、そもそもデータ収集を行った全集団と、実際に解析に用いることができた解析集団をそれぞれ列に入れ込むことで、どのような対象者が”選択”されたのか、そしてそこに選択バイアスのリスクがないかを判断する一助となります。
たとえば、先ほどの図ではPoint 1の「Response sampleとComplete sample」がそれに該当します。
選択バイアスが生じる原理にもサンプリングによるバイアス、欠損によるバイアスと幾つかありますが、ここで問題にするのは欠損によるバイアスです（サンプリングによ選択バイアスの影響を測定するためにはTarget populationにおける対象者背景の分布を記述せねばならないが、それは不可能なことが殆どのため）。
一方、欠損によるバイアスであれば「調査対象となった全集団（Response sample）」と「最後まで追跡できた部分集団（Complete sample）」を記述する形で選択バイアスの影響を部分的に調べることができます。
選択バイアスですが、「追跡に成功した群と失敗した群の2群間で曝露の有無の割合が異なり、さらにアウトカムの原因となる因子の割合がことなる」ことでしょうじます。
何を言ってるかわからないと思うのでイラストにするとこんな感じです。
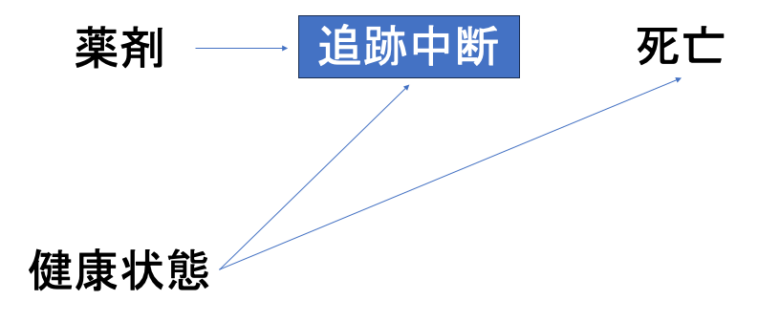
薬剤あり vs なし群で死亡リスクを比較したいとしましょう。
この時、薬剤投与群は有害事象が発症することでより高い脱落リスクを抱えているとします。
また、元々の健康状態が悪い人ほど脱落しやすく、さらにアウトカムである死亡が発生しやすかったとします。
この時、追跡中断の対象者は除外し、最後まで追跡し続けられた対象者を”選択”して解析しました。
すると、この”選択”された集団における薬剤曝露群とは「副作用があるにも関わらず薬剤を使い続けられるほど元々の健康状態が良かった対象者」となります。
すなわち、曝露群は死亡リスクが低い患者となり、favorable to 曝露群な選択バイアスが生じます。
ちょっとラフな言い方をすると、調査対象としていた全集団に対して解析の対象として”選択”された集団が質的に異なっていたことでバイアスが生じているわけです。
となると、Columnに全集団・解析集団を記載し、両者で対象者背景の分布に差異がないかをアセスメントすることで、選択バイアスの有無をある程度は評価することができます（上の図でいうと、”健康状態→選択”のパスの有無をアセスメントする）。
この時、特に大切になるのがアウトカムにおける対象者選択です。
このイラストの通り、選択バイアスが成立する条件の一つは「選択された集団とそうではない集団でアウトカムに影響する因子の分布が異なる」でした。
ですから、全集団と解析集団においてアウトカムの発症頻度などが異なっていた場合、それは「アウトカムのリスクとなる何らかの因子に基づいて対象者選択が行われた可能性がある」ことを示唆します。
つまり、選択バイアスの影響を示唆するということですね。
外的妥当性の観点から
さて、お次は外的妥当性です。
選択バイアスで述べたこととオーバーラップしますが、ここでも調査対象としていた全集団、そして実際に解析の対象となった解析集団それぞれのColumnを記載し、両集団における対象者特性の分布を比較することで、「解析集団における結果が、調査対象にした全集団に対しても外挿可能であるか」というアセスメントの一助となります。
いずれかの変数の分布が異なっており、さらにその変数がEffect modifierである場合には、解析結果を全集団に外挿することができません。
また、解析集団内にEffect modifierが存在する場合にはEffect modifierのカテゴリーごとにColumnを作り、さらにその中で曝露・非曝露の2群を記述する必要があります。
たとえば、性別がEffect modifierになると仮定した場合には、男女それぞれで曝露・非曝露群の対象者特性を記述するという感じですね。
質の高い行の描き方
お次は行、英語で言えばRow、対象者背景などの変数の分布を記載していきます。
ここで考えるべきは「対象者特性のうちどのような変数を記述するか」ということですね。
主に記述されるのは以下の変数になります。
- 最終解析に投入された変数
- 潜在的な交絡因子と考えられる変数
- 対象者の選択に使われた変数（サンプリングに使われた変数、欠損や調査参加に影響しうる変数）
- 効果修飾因子
- アウトカム
そしてさらに考えるべきは「それらの変数をどのような統計量で記述するか」ということ。
連続値かカテゴリー値か、などですね。
連続値で測定された変数をそのまま連続値として使用する場合、これは平均＋SD、平均値＋四分位範囲などで良いでしょう（データが正規分布していない際には、加えて最大値・最小値、中央値などを提示するとinformativeです）。
一方、連続値をカテゴリー値に変換した場合は配慮が必要で、この場合はオリジナルの連続値の変数もTable 1に記述することが推奨されています。
なぜなら、カテゴリーの閾値が適切に設定されなかった場合には誤測定や残差交絡の問題が起こるリスクがあるからです。
そのようなリスクをアセスメントするため、以下のTable 1のPoint 6ではオリジナルの連続値と変換後のカテゴリー値の双方を記述しています。
終わりに
たかがTable 1、されどTable 1。
これまであたりまえのように描いてきたTable 1ですが、「内的妥当性・外的妥当性」という視点から光をあてると、こんなに奥深く考えることができるなんてとっても面白いですよね。
これは完全に私の感想ですが「論文を1本読むだけで普段当たり前にやっていることへの理解がこんなにも深まるんだから、やっぱり勉強してると良いことあるなぁ」としみじみと思ったのでした。
本記事が参照にした元論文ではより深く解説されておりますので、ぜひぜひそちらもご覧ください。
終わりにその２
私は外資系企業と国立大学の疫学専門家として活動しておりますが、それ以前はブラック企業に勤める社畜として上司に怒鳴られる日々を送っていました。
「強く生きるには専門性だ」
そう一念発起し、大学院の修士課程に通い、そこから2年間で疫学専門家としてのキャリアにルートインし、2年で年収を1,400万アップさせることができました。
こちらのnoteでは、疫学の世界で活躍したいと考える方々に向けて、「専門性ゼロの段階からどうやって企業の疫学専門家のポジションをゲットするか」ということを解説します。
私自身が未経験から2年間で外資系企業の疫学専門家になるまでに積み重ねた経験、ノウハウの全てをお伝えするつもりで書き綴っています。
「これを読めば、企業の疫学専門家になるために必要な知識は全て揃う」
その気合いで、私のノウハウを全てお伝えします。
すきとほるからのお願い
本ブログは、読者の方が自由に記事の金額を決められるPay What You Want方式を採用しています。
学生さんや経済的に厳しい方からはお金を取りたくなく、それが経済格差に起因する学力格差へと繋がると考えるからです。
仕事の合間に記事を書く時間を見つけるのはちょっぴり大変ですが、今後も皆様の「研究生活をほんのり豊かに」できる記事をお届けし続けたいと思っております。
なのでお金に余裕があり、そして「勉強になった！」、「次も読みたい！」と本ブログに価値を感じてくださった場合は、以下のボタンをクリックし、ご自身が感じた価値に見合うだけの寄付を頂戴できますと幸いです。
励みになるので、ご寄付はとてもありがたいです！
引き続き情報発信していく活力になりますので、ぜひお気持ちに反しない範囲でご寄付をお願い致します！
