こんにちは、すきとほる疫学徒です。
データベース研究においては、曝露やアウトカムを定義するために設定した条件(アルゴリズム)が「本当に見たいものを正しく定義できているか」というアルゴリズムの妥当性を考える必要があります。
おそらく、ここまでは皆さん「そりゃそうだろう」とご納得頂けるでしょう。
では、主たる指標のうち、どの指標をどの状況で優先すべきでしょうか？
ご存知の通り、感度と特異度、PPVとNPVはトレードオフの関係になるため、「アルゴリズムAでは感度が向上するが、アルゴリズムBでは特異度が向上する」という状況は珍しくありません。
この時、アルゴリズムAとアルゴリズムBのどちらをプライマリーのアルゴリズムに設定しますか？
今回の記事では、アルゴリズムを設定した変数や、状況に応じて、「この指標が優先されるべき」ということを解説していきたいと思います。
なお、本記事は以下の文献を参考に執筆されています。
妥当性指標間のトレードオフについて
指標間の優先順位の話をする前に、それぞれの指標、およびそれらの間のトレードオフについておさらいしましょう。
心筋梗塞という病名の妥当性を確かめるためのバリデーション研究について考えます。
あなたの目の前に電子カルテと、診療報酬請求データベースがあるとします。
この時、あなたがデータベース研究で使用するのは診療報酬請求データベースのみですが、一部の患者において電子カルテにアクセスが可能であったため、「診療報酬請求データベースで定義した心筋梗塞が、どれだけ正しいのか」ということを確かめるため、電子カルテを使用できるとしましょう。
なお、電子カルテに記載されている診断名は全て正しい（ゴールドスタンダード）とします。*
*実際の医療現場では、電子カルテに記載されている診断名が本当に正しいとも限らないため、バリデーション研究を行う際には、その分野の専門医の医師2名が独立して電子カルテを調べ、その患者が本当に心筋梗塞の患者であるかどうかという判定を行い、ゴールドスタンダードを決定します。この際も、診断基準を作成したり、2名の意見が分かれた際の最終決定者としてさらに別の専門医を用意したりと、ゴールドスタンダードの決定は非常に手間がかかります。
さて、そんなこんなでゴールドスタンダード側の心筋梗塞が定義できたとしましょう。
これで、あなたの手元には
- 診療報酬請求データベースで定義された心筋梗塞（algorithm positive）
- 診療報酬請求データベースで定義された非心筋梗塞（algorithm negative）
- 電子カルテにおける心筋梗塞（true positive）
- 電子カルテにおける非心筋梗塞（true negative）
という4種類の診断があることになります。
| 診療報酬請求データ心筋梗塞 | 診療報酬請求データ非心筋梗塞 | |
| 電子カルテ心筋梗塞 | a | b |
| 電子カルテ非心筋梗塞 | c | d |
この時、
- 感度：a/(a+b)*100
- 特異度：d/(c+d)*100
- 陽性的中度（PPV）：a/(a+c)*100
- 陰性的中度（NPV）：d/(b+d)*100
でしたね。
つまり、
感度とは、真の心筋梗塞患者のうち、どの程度を正しく”心筋梗塞あり”と定義できているかという指標であり、
PPVとは、”心筋梗塞あり”と定義された者のうち、どの程度が真の心筋梗塞患者であるかという指標です。
そして数式を見て頂ければわかる通り、特異度・NPVはそれぞれ感度・PPVの裏返しであり、非心筋梗塞患者に着目した指標です。
さて、妥当性指標の基本的な説明が終わったところで、それらの指標間のトレードオフの説明に入ります。
再び、心筋梗塞患者を診療報酬請求データベースから正しく抽出したいというモチベーションがあったとしましょう。
この時、”正しく”という言葉が「感度を上げる」ことを指すのか、「特異度を上げる」ことを指すのかで目指すべきアルゴリズムの形が変わってきます。
下の図はを見てください。
黒い四角の内側：全患者
赤丸：真の心筋梗塞患者
青丸：真の非心筋梗塞患者
オレンジ丸の内側：アルゴリズムにより定義された心筋梗塞患者
オレンジ丸の外側：アルゴリズムにより定義された非心筋梗塞患者
です。
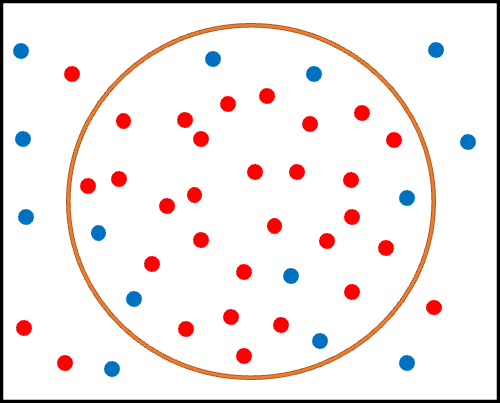
さて、この時2つの定義によるアルゴリズムを考えましょう。
一つ目は、ICD-10 code: I21のみによるシンプルな定義です。
これは非常にシンプルな定義のため、多くの患者が”心筋梗塞あり”と判定されることになります。
これにより、より多くの患者がオレンジ丸の中に含まれることになったため、オレンジ丸の外側の赤丸の数は僅かであることが見て取れます。
これが、”感度が高い（真の心筋梗塞患者の取りこぼしがない）”状態です。
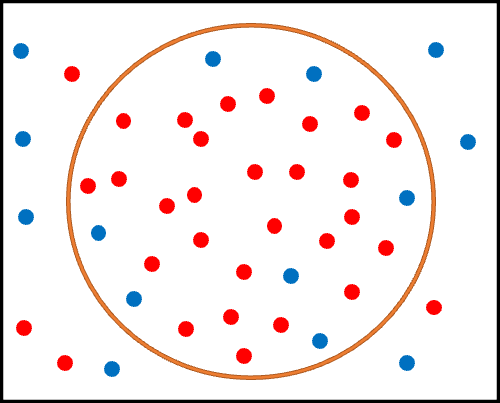
では、二つ目の定義を考えてみましょう。
一つ目のシンプルな定義では、緩やかなアウトカム定義を設けたため、真の心筋梗塞患者（赤丸）の取りこぼしは多くありませんでした。
一方で、青丸の取りこぼしが多くなってしまっています。
青丸は、真の非心筋梗塞患者ですから、本来であればオレンジ丸の外（アルゴリズムにより定義された非心筋梗塞患者）に位置していなければなりません。これはつまり、特異度が低い状態を指します。
特異度の低さを嫌った研究者らは、アルゴリズム定義を修正することにしました。
より多くの青丸がオレンジ丸の外に位置すればいいわけですから、やるべきことはオレンジ丸の大きさを小さくすることです。
心筋梗塞のアルゴリズムで言うならば、より複雑な条件を設定し、”心筋梗塞あり”と判定される患者を少なくするということですね。
例えば、ICD-10 code: I21に加えて、心筋梗塞の診断に必要な検査X、そして心筋梗塞患者の大多数に投与される薬剤Yも定義に追加したとしましょう。
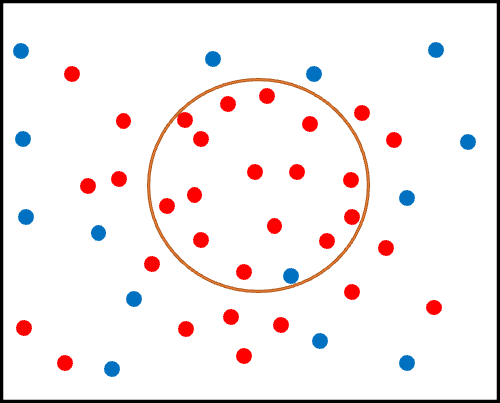
これをイメージにすると、以下です。
オレンジ丸が小さくなり、その中に含まれる青丸の数（真の非心筋梗塞なのに、誤って心筋梗塞と判定されてしまった患者）が少なくなったことがわかるかと思います。
これにより、特異度が上昇しました。
一方で、オレンジ丸の中に含まれる赤丸の数（真の心筋梗塞であり、正しく心筋梗塞と判定された患者）が少なくなってしまったので、感度は下がることになります。
さて、感度・特異度がトレードオフの関係にあるということがお分かり頂けたでしょうか？
抽象的な話だけだと分かりにくいかもしれないので、日本で実際に行われたバリデーション研究を紹介しましょう。
この研究では、新潟大学病院の電子カルテをベースに診断された疾患をゴールドスタンダードにし、健保データベースで定義された疾患の妥当性を確かめています。
筆者らは、6つの疾患それぞれに対し、9つのアルゴリズムを作成しました。
DPCデータのICD-10 codeのみのアルゴリズム、DPCデータのICD-10 code + 薬剤コードによるアルゴリズム、DPCデータのICD-10 code + 処置コードによるアルゴリズムなどです。
そのうち、心不全を特定するために作成したアルゴリズムでは、
ICD-10 codeのみ：感度100%/特異度90.1%
ICD-10 code + 薬剤コード: 感度93.3%/特異度100%
という結果になりました。
説明した通り、より厳しいアルゴリズムを用いることで、感度が下がり、特異度が上がっていることがお分かり頂けたかと思います。
これが、妥当性の指標間のトレードオフです。
指標間の優先順位について
さて、思いのほか前置きに文字数を割いてしまい、若干息が切れかかっていますが、ここからがメインの内容になります。
あなたがデータベース研究の責任者である疫学専門家であり、心不全を正しく判定するアルゴリズムを作成せねばならなかったとしたら、上の2つのアルゴリズムのうち、どちらをプライマリーに設定しますか？
”感度も特異度もアルゴリズムAの方がBより高い”という状況であれば、何の迷いもなくアルゴリズムAを選択できるでしょう。しかしながら、感度と特異度はトレードオフ、「あちらを立てればこちらが立たぬ」という状況です。
さて、どちらを選びますか？
この答えは、以下のように状況に応じて変わってきます。
感度が特に重要になる状況
感度とは、「コホート全体における真の陽性患者のうち、アルゴリズムがどれだけ正しく陽性と判定できるか」という指標でした。
図にするならば、黒い四角内の赤丸のうち、オレンジ丸の中に含まれる赤丸の割合です。
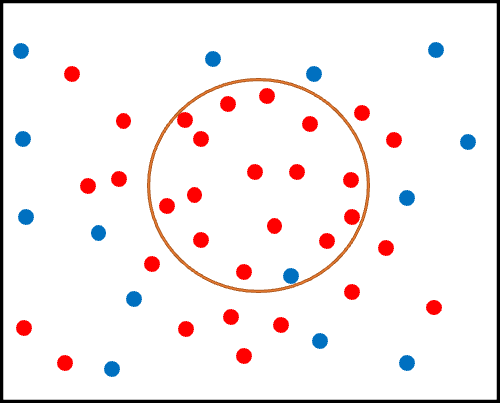
さて、この感度が優先されるのはどのような状況でしょうか？
それは、「真の陽性患者をより多く発見するメリットが、真の陰性患者を誤って陽性と判定してしまうデメリットを上回る状況」です。
具体的には以下になります。
研究の経済的・時間的コストを削減できる場合
例えば、乳がん患者をコホートにした研究を行う際に、診療報酬請求データでの患者特定→電子カルテレビューでの特定、というように2段構えの患者抽出が行える状況だったとしましょう。
潜在的な患者コホートは1000名とします。
この時、診療報酬請求データでの患者特定をせずに、いきなり電子カルテレビューに入ってしまうと、1000名分もの電子カルテをレビューせねばならず、膨大な時間とお金がかかります。
そこで、一段階目で感度100％、特異度60％のアルゴリズムを用いて、患者抽出を行なったとしましょう。
仮定として、1000名のコホートのうち、真の乳がん患者は150名だったとします。
このアルゴリズムによって患者抽出を行うと、
150名の真の乳がん患者は全て抽出される一方、850名の真の非乳がん患者からは40％が乳がん患者として抽出されることになります（特異度が60％なので、真の非乳がん患者のうち40％は誤って乳がん患者と判定される）。
すると、抽出後のコホートは
150*100% + 850*40% = 490
となり、当初の1000名よりも大幅に電子カルテレビューの対象となる患者数を減らすことができました。
より広範な患者を包含することが必要な状況
感度が低く、特異度が高いアルゴリズムを使用すると、基本的にはより重症な患者ほど正しく陽性と判定されやすくなります。
そのため、感度が高いアルゴリズムを用いて患者抽出を行うことで、軽症から中等症の患者も取りこぼさずにコホートに含むことができます。
例えば、とある薬剤Aの有効性・安全性を測定したい時、もし感度が低いアルゴリズムを用いてベースとなるコホートの抽出を行なってしまうと、そのコホートは比較的重症な患者で形成されたコホートとなってしまいますよね。
これにより、研究結果の一般化可能性が低下することになります。
ちなみにこの文脈で言うと、私は有害事象の頻度を明らかにするというモチベーションで研究を行う際も、感度を優先したアウトカム定義を使用するべきだと思っています。
有害事象においては、「実際より少なく」報告される方向にバイアスがかかるより、「実際より多く」報告される方にバイアスがかかった方が、患者にとって有益な意思決定につながるという考えです。
ただ、頻度の低い有害事象を対象にする場合は、感度の高さよりも特異度の低さの方がセンシティブにアウトカムの誤測定に影響してしまうので、あまりにも特異度が低い場合には注意が必要だと思います（詳しくは次の項を参照してください）。
全コホートに占める曝露群の割合が多い時に、曝露を特定する状況
状況として、アウトカムは完璧に定義できており、曝露においてnon-differencialな測定誤差が発生している状況があるとしましょう。
この時、感度の高さ（特異度の低さ）が薬剤曝露の因果効果を測定する解析において、どのような影響を与えるかを考えます。
全コホート1000名のうち、薬剤曝露を受けた患者が80％いたとします。
この時、感度90％、特異度50％のアルゴリズムを用いて曝露を判定すると、判定上は
曝露群：800*90% + 200*50% = 820名（真の曝露群は800名）
被曝露群：200*50% + 800*10% = 180名（真の非曝露群は200名）
と判定されます。
ご覧の通り、このように真の曝露群の割合が高い時には、感度が高ければ、特異度が低くとも曝露の誤測定の影響が小さいということがお分かり頂けるかと思います。
では、真の曝露群の割合が低い時にはどうなるでしょうか？
全コホート1000名のうち、薬剤曝露を受けた患者が20％しかいなかったとします。
この時、先ほど用いたこの時、感度90％、特異度50％のアルゴリズムを用いて曝露を判定すると、判定上は
曝露群：200*90% + 800*50% = 480名（真の曝露群は200名）
被曝露群：800*50% + 200*10% = 420名（真の非曝露群は800名）
と判定されます。
ご覧の通り、曝露の誤測定の影響が非常に大きくなってしまっていることがお分かり頂けるかと思います。
この場合では、感度の高さよりも、特異度の低さの方が曝露の誤測定に与える影響が強く出てしまっているわけですね。
以上のことから分かる通り、全コホートに占める真の曝露やアウトカムを有する患者の割合が多い場合には、特異度よりも感度を優先した方が、曝露の誤測定のインパクトが小さくなると言えます。薬剤を曝露にする際などは、曝露：非曝露群を1:1で抽出することが多いため、コホートに占める曝露群の割合も大きくなります。そのため、感度のインパクトが大きくなりますので、薬剤を曝露に設定する状況では、感度を優先することが多くなるでしょう。
特異度が特に重要になる状況
薬剤Xの曝露群・被曝露群において疾患Yのリスクを比較したとします。
この際、疾患Yを定義するアルゴリズムにおいて感度が変化したとしても、その測定誤差がnon-differencialであればリスク比に影響はありません。
100名の曝露群における疾患Yの発症者が50人、同じく100名の被曝露群における疾患Yの発症者が25人としましょう。
リスク比は、
50/100 ÷ 25/100 = 2.0
となりますが、ここで疾患Yを定義するアルゴリズムの感度が50％になったとすると、リスク比は
50*50%/100 ÷ 25*50%/100 = 2.0
で、感度にどのような数字がこようと、計算上でキャンセルアウトされますので、リスク比に影響がないということがお分かり頂けるかと思います。
一方、特異度が変化した場合はどうでしょうか？
曝露群・被曝露群、両群の真の疾患Y発症者数は同じだとして、感度を100％固定し、特異度がnon-differentialに50％まで低下した状況を考えてみましょう。
リスク比は、
(50 + 50*50%)/100 ÷(25 + 75*50%)/100 = 1.2
と大幅に低下します。
このことから、アウトカムを定義し、リスク指標を算出する際には、感度よりも特異度を優先した方が良いということがわかります。
PPVが特に重要になる状況
PPVが重視されるのは、特定の疾患を持つ患者集団からなるコホートを作成したい時です。
PPVが高いということは、その定義により抽出された疾患群において、真の非疾患患者の割合が低くなるということですので、PPVを上げることで、より純度の高いコホートを作成することができます。
下図のオレンジ丸の中の赤丸の割合がPPVですね。
ただ、感度のところで言ったことを思い出してください。
基本的に感度とPPVはトレードオフの関係にあるため、PPVを上げることで感度は下がります。
これにより、疾患Yからなるコホートを作成した際に、より重症な疾患Yの患者ばかりが抽出されてしまい、結果的にコホートの一般化可能性が低下してしまうという問題が生じます。
コホートを、たとえ重症化患者ばかりになっても正しく疾患を有する患者だけで構成したいのか、それとも一般化可能性の観点から軽症・中等症の患者も含めたいのか、これによって感度、PPVのどちらを優先するかが決まってくるでしょう。
NPVが特に重要になる状況
コホート形成における患者の除外基準の定義において、NPVは重要になります。
例えば、薬剤Xと疾患Yの関連を見る際に、コホートに疾患Zを持っている患者を含めてしまうと、交絡バイアスが生じるとしましょう。
疾患Zの患者は、薬剤Xを投与されやすく、かつ疾患Yを発症しやすいという状況です。
この時、疾患Zを除外して、残ったコホートにおいて、疾患Zを持つ患者の割合を減らしてやらねばなりません。
つまり、疾患Zではないと判定された患者において、真の非疾患Zの患者が高頻度で存在する、言い換えると高いNPVが必要になります。
下図で言うと、オレンジ丸の中が疾患Zと判定された患者ですから、除外されずにコホートに残るのは、オレンジ丸の外側の患者ですね。NPVが高いというのは、このエリアにおける全患者のうち、青丸の割合が高い状況です。
下図ですと、オレンジ丸の外側にも沢山の赤丸が残ってしまっているので、これは「本来は除外せねばならない疾患Zの患者が、除外されずにコホートに残ってしまっている状況」となります。
これでは疾患Zによる交絡バイアスの影響を適切に処理できません。
このように、特定の条件を持つ患者を適切に除外したい時には、NPVの高いアルゴリズムを用いる必要があります。
終わりに
いかがでしたでしょうか？
最近はデータベース研究が盛んになってきており、アルゴリズムの妥当性にも注意が払われるようになってきましたが、「妥当性のうちどの尺度を、どの状況で優先するか」という情報は、まだ日本語ではあまり出回っていないように思いました。
そのため、解説ブログを書いてみた次第です。
楽しんで頂けましたら幸いです。
すきとほる疫学徒からのお願い
本ブログは、読者の方が自由に記事の金額を決められるPay What You Want方式を採用しています。
「勉強になった！」、「次も読みたい！」と本ブログに価値を感じてくださった場合は、以下のボタンをクリックし、ご自身が感じた価値に見合うだけの寄付を頂戴できますと幸いです。
もちろん価値を感じなかった方、また学生さんなど金銭的に厳しい状況にある方からのご寄付は不要です。
引き続き情報発信していく活力になりますので、ぜひお気持ちに反しない範囲でご寄付をお願い致します！
